0. Modèlisation par regression linéaire

1. L'équation de la droite de régression

2. Variance des résidus et aléa expérimental

3. x prédit et sa variance

4. Coef de correl. et coef. de détermination

5. Bibliographie

0. Modélisation par régression linéaire

---

La méthode de mesure va être considérée comme une boite noire.

Appelons variable x, les valeurs que peuvent prendre des étalons purs de la substance S à mesurer. Appelons y les signaux de sortie donnés par la méthode de mesure. L’étalonnage par régression linéaire s’utilise lorsqu’on a montré qu’il est pertinent d’utiliser le modèle suivant d’explication des y par les x :

y = f(x) + e     = a0 + a1x+ e	• f(x) = a0 + a1x est la fonction de réponse déterministe de la méthode de mesure. Dans ce chapitre, on s’intéresse au cas ou la fonction est considérée comme linéaire. • e est une variable aléatoire qui représente la partie aléatoire irréductible associé aux mesures.
D’un point de vue statistique x est dite variable explicative ou indépendante. Y est dite variable expliquée ou dépendante dépendante (les valeurs de y sont causées par les valeurs de x).

Le principe de l'étalonnage par régression linéaire consiste à :
- 1) fabriquer un certain nombre d'étalons de la substance S à doser qui prendront des valeurs connues x_i ;
- 2) puis obtenir les valeurs y_i correspondantes en appliquant pratiquement de façon conforme la méthode de mesure ;
- 3) puis à calculer les coefficients a₀ et a₁ de la fonction de réponse linéaire.

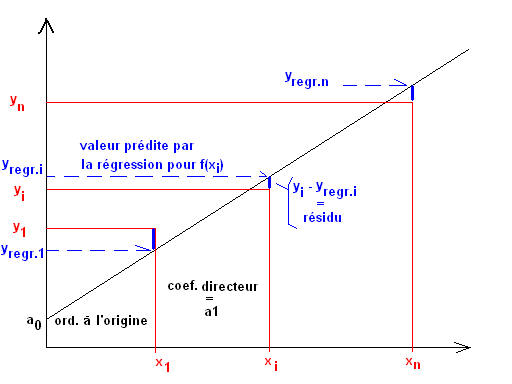
Pour cela, on va utiliser un calcul dit calcul de régression linéaire par la méthode des moindres carrés. Il s'agit de calculer les coefficients a₀ et a₁ qui minimisent la somme des carrés des distances entre les valeurs observées y_i et la droite d'équation y_regr = a₀ + a₁x

Les calculs de la méthode des moindres carrés supposent 2 propositions fondamentales :
- 1) Le modèle déterministe pur (sans aléa) y = a₀ + a₁x est pertinent sur le domaine des valeurs de x étudiées.
- 2) L'aléa e est une variable loi normale de moyenne nulle et d'écart-type σ à l'identique sur tout le domaine des mesures (où si l'on préfère, l'aléa e_i sur chaque signal y_i obtenu sur chaque x_i suit la même variable aléatoire normale de moyenne nulle et d'écart-type σ). Et les aléas sont indépendants : il n'y a pas d'influence de l'aléa d'un mesurage sur l'aléa d'un autre mesurage.

A ceci, on peut rajouter cette caractéristique (bien embétante) de la méthode des moindres carrés : la méthode n'est pas une méthode robuste. En effet, l'utilisation de la somme des carrés des distances donne un poids plus élevé aux points qui s'éloignent du modèle linéaire : les éventuelles mesures aberrantes non décelées et non éliminées conduiront à un effet indésirable maximal !